Diffusion Modelサマリー

1. はじめに

2020年にDiffusion Modelに関する論文が発表されて以降、生成モデルの研究が進展している。 2021年以降はこのDiffusion Modelをベースとした画像生成AIサービスがリリースされて世間からの注目を集めている。

2023年5月現在生成モデルとして最も注目を集めているのは大規模言語モデル(例: OpenAIのGPT-4)であるが、Diffusion Modelは主に画像生成の文脈で利用されており、モデルのスコープが異なることに注意されたい。

最近のバズワードの大規模言語モデルではないが、生成モデルという枠組みの中では非常に重要かつモデル構造も面白いので、今回はDiffusion Modelを取り扱っていきたい。

  • TransformerベースにGPTモデルファミリーまで一気に論文読む&実装する会も将来的に扱うつもり。

2. Diffusion Model 早わかり

Diffusion Modelは生成モデルの1種であり、forward processとreverse processの２つの確率過程から構成される。

平たく言えば下記の図のようになる。

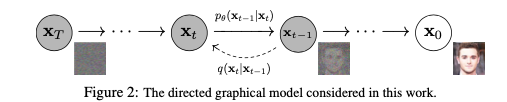
Diffusion Modelイメージ(Ho et al.(2020)より引用)

  • forward processは画像に僅かなノイズを少しずつ加えるプロセスを示している。
  • reverse processはノイズになったデータから徐々に元の画像に復元するプロセスを示している。
    • このreverse processをモデル化してデータから学習する

実際に学習したモデルを用いて、画像生成する場合には何らかのノイズをモデルに与えて、reverse processを経由することで、画像が生成される。Ho et al.(2020)は下記のような生成結果を提示している。

生成結果(Ho et al.(2020)より引用)

なお、最近の研究ではテキストを入力すると対応する画像が生成されるモデルも存在している。

生成結果(Ho et al.(2020)より引用)

このような生成は条件付き生成と呼ばれ、実務上求められるのはこちらの生成方法だろう。

なぜこのようなシンプルな構造でうまくいくのか？については現在も明確な答えはないが、最もシンプルな仮説は下記である。

  • reverse processが多くの確率層からなる深いネットワークであることが複雑な画像生成を実現している
    • 初期の画像処理モデルも層を深くすることが出来る様になってブレイクスルーが起きた(例: ResNet)
  • 生成プロセス(reverse process)のみをモデル化している
    • VAEは生成モデルと認識モデルを同時に学習
    • GANは生成モデルと認識モデルを交互に学習

それでは以降では具体的なモデルの中身を見ていきたい。

3. Diffusion Model モデル詳細

本章では岡野原(2023)に基づいてDiffusion Modelの全体像・学習・推論を見ていく。

  • 余談: Ho et al.(2020)を見ていってもよいが、いきなりこれを見ると挫折する。やや遠回りに見えるがLuo et al.(2022)から読み進めていくことを勧める。

3.1 全体像

2で述べたようにDiffusion Modelはforward processとreverse processから構成される。

forward process

forward processはもともとのデータ $\bold{x}_0$ から徐々にデータの情報を減らしてノイズを加えた、ノイズ付与データの系列 $\bold{x}_1, \cdots, \bold{x}_T$を得るマルコフプロセスである。

  • $q(\bold{x}_{1:T} \mid \bold{x}_0)= \prod_{t=1}^{T} q(\bold{x}_t \mid \bold{x}_{t-1})$

  • $q(\bold{x}_t \mid \bold{x}_{t-1}) = \mathcal{N}\left(\bold{x}_t; \sqrt{\alpha_t}\bold{x}_{t-1}, \beta_t\bold{I}\right)$

ここで$0 < \beta_1 < \cdots < \beta_T < 1$は分散の大きさを制御するパラメータで$\alpha_t = 1- \beta_t$とする。　$\alpha_t$は情報をどれだけ保持するかを示しており、これらを合わせてノイズスケジュールと呼ぶ。

なお任意の$\bold{x}_0$についてTが十分大きい時$q(\bold{x}_{T} \mid \bold{x}_{0}) \approx \mathcal{N}\left(\bold{X}_{T}; 0, \bold{I}\right)$と$q(\bold{x}_{T}) \approx \mathcal{N}\left(\bold{x}_{T}; 0, \bold{I} \right)$が成立する。

なお、ノイズに正規分布を使っていることから、各時刻$t$におけるサンプル$\bold{x}_t \sim q\left(\bold{x}_t \mid \bold{x}_0\right)$は解析的に求めることが出来る。

  • $q\left(\bold{x}_t \mid \bold{x}_0\right) = \mathcal{N}\left( \sqrt{\bar{\alpha}_t}\bold{x}_{0}, \bar{\beta}_t\bold{I}\right) $
  • $\bar{\alpha}_t = \prod_{s=1}^{t}\alpha_s$
  • $\bar{\beta}_t = 1 - \bar{\alpha}_t$

証明は岡野原を参照されたいが、帰納的に求めることが出来る。

reverse process

reverse processは完全なノイズからデータに戻るためのマルコフ過程として定義する。 この時各ステップは正規分布であると仮定し、平均と共分散行列をNNでモデル化する。このときの入力は時刻$t$と前の時刻の変数$\bold{x}_{t}$である。

  • $ p_{\theta}(\bold{x}_{0:T}) = p\left(\bold{x}_T\right) \prod_{t=1}^{T} p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_t) $
  • $p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_t) = \mathcal{N}\left(\bold{x}_{t-1}; \mu_{\theta}(\bold{x}_t, t), \bold{\Sigma}_{\theta}(\bold{x}_t, t)\right)$
  • $p\left(\bold{x}_T\right) = \mathcal{N}\left(\bold{x}_{T}; 0, \bold{I}\right)$

この仮定は徐々に画像にガウシアンノイズを加えるプロセスを最終的に画像がガウシアンノイズになるまで続けることを意味している。

3.2. 学習

Diffusion Modelのパラメータは最尤法によって推定される。 したがって観測変数 $\bold{x}_{0}$ の尤度$p_{\theta}(\bold{x}_{0})$の最大化を行えばよい。 この時$p_{\theta}(\bold{x}_0)$はreverse processの同時確率において$\bold{x_1}, \cdots, \bold{x}_T$を周辺化することで得られる。

$$p_{\theta}(\bold{x}_0) = \int p_{\theta}(\bold{x}_{0:T})d \bold{x}_{1:T}$$

ここで $\bold{x}_{i:j} = \bold{x}_i, \cdots, \bold{x}_j$である。　

単純にこの尤度を最大にしたいのだが、潜在変数の積分が含まれていることが問題である。この積分計算があるせいで、現実的な計算時間で計算することが難しくなってしまう。

そこでDiffusion Modelに限らず生成モデルの多くは対数尤度の変分下限(ELBO)の最大化によってパラメータの推定を行う。

以降は目的関数となるELBOの定式化を行う。なお最小化問題として定式化するために以下では負の対数尤度、ELBOを考える。

$$ \begin{aligned} - &\log p_{\theta}(\bold{x}_0) \\ &= \log \int \frac{q(\bold{x}_{1:T} \mid \bold{x}_{0}) p_{\theta}(\bold{x}_{0:T})}{q(\bold{x}_{1:T} \mid \bold{x}_{0})} d \bold{x}_{1:T}　\\ &\le \mathbb{E}_{q(\bold{x}_{1:T}\mid \bold{x}_{0})} \left[- \log \frac{p_{\theta}(\bold{x}_{0})}{q(\bold{x}_{1:T}\mid \bold{x}_{0})} \right] \quad\text{(Jensenの不等式と期待値定義より)} \\ &=\mathbb{E}_{q(\bold{x}_{1:T}\mid \bold{x}_{0})} \left[- \log \frac{ p_{\theta}(\bold{x}_{0} \mid \bold{x}_{1}) \dots p_{\theta}(\bold{x}_{T-1} \mid \bold{x}_{T})p(\bold{x}_{T})} {q(\bold{x}_{T} \mid \bold{x}_{T-1})q(\bold{x}_{T-1} \mid \bold{x}_{T-2})\dots q(\bold{x}_{1} \mid \bold{x}_{0})} \right] \\ &= \mathbb{E}_{q(\bold{x}_{1:T}\mid \bold{x}_{0})}\left[ - \log p(\bold{x}_{T}) - \sum_{t \ge 1} \log \frac{p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_{t})}{q\left(\bold{x}_{t} \mid \bold{x}_{t-1}\right) } \right] \quad \text{(対数の性質より)} \\ &:= L(\theta) \end{aligned} $$

ここで$L(\theta)$対数尤度の下限であることからELBOと呼ばれる。

ここからELBOをもう少し変形して、更に計算しやすくする。 $$ \begin{aligned} L(\theta) &= \mathbb{E}_{q(\bold{x}_{1:T}\mid \bold{x}_{0})} \left[- \log p(\bold{x}_{T}) - \sum_{t>1} \log \frac{p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_{t})}{q\left(\bold{x}_{t} \mid \bold{x}_{t-1}\right) } - \log \frac{p_{\theta}(\bold{x}_{0} \mid \bold{x}_1)}{q\left(\bold{x}_{1} \mid \bold{x}_{0}\right) } \right] \\ &= \mathbb{E}_{q(\bold{x}_{1:T}\mid \bold{x}_{0})} \left[- \log p(\bold{x}_{T}) - \sum_{t>1} \log \frac{p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_{t})}{q\left(\bold{x}_{t-1} \mid \bold{x}_{t}, \bold{x}_{0} \right) } \times \frac{q(\bold{x}_{t-1} \mid \bold{x}_{0})}{q(\bold{x}_{t} \mid \bold{x}_{0})} - \log \frac{p_{\theta}(\bold{x}_{0} \mid \bold{x}_{1})}{q\left(\bold{x}_{1} \mid \bold{x}_{0}\right) } \right] \quad\text{(ベイズの定理より)} \\ &= \mathbb{E}_{q(\bold{x}_{1:T} \mid \bold{x}_{0})} \left[- \log \frac{p(\bold{x}_{T})}{q(\bold{x}_{T} \mid \bold{x}_{0})} - \sum_{t>1} \log \frac{p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_{t})}{q\left(\bold{x}_{t-1} \mid \bold{x}_{t}, \bold{x}_{0}\right) } - \log p_{\theta}(\bold{x}_{0} \mid \bold{x}_{1}) \right] \quad\text{(連鎖的に簡略化出来る)}\\ &=\mathbb{E}_{q(\bold{x}_{1:T}\mid \bold{x}_{0})} \left[ \underbrace{D_{KL}(q(\bold{x}_{T} \mid \bold{x}_{0}) \mid\mid p(\bold{x}_{T}))}_{L_{T}}+ \sum_{t>1} \underbrace{D_{KL}(q(\bold{x}_{t-1} \mid \bold{x}_{t}, \bold{x}_{0}) \mid\mid p(\bold{x}_{t-1}\mid \bold{x}_{t}))}_{L_{t-1}} - \underbrace{\log p_{\theta}(\bold{x}_{0} \mid \bold{x}_{1}) }_{L_{0}} \right] \end{aligned} $$

具体的な$L_T$, $L_{t-1}$, $L_{0}$の計算結果については時間の都合上省略する。今後記載アップデート予定。実はここが非常に重要。

最終的にはDiffusion Modelの学習に使う目的関数は次のように書くことが出来る。 $$ L_{\gamma}(\theta) = \sum_{t=1}^{T} w_{t} \mathbb{E}_{\bold{x}_{0}, \epsilon} \left[ \mid\mid \epsilon - \epsilon_{\theta}\left(\sqrt{\bar{\alpha}_{t}}\bold{x_{0}} + \sqrt{\bar{\beta}_{t} \epsilon}, t\right) \mid\mid^2\right] $$

ここで$\gamma = [w_1, \ldots, w_T]$であり、それぞれは各時刻の重みを示す。なおHo et al.(2020)では$w_t$をすべて1として学習している。

  • 岡野原では重みの設定によらず目的関数の最適解が一致すること、重みの設定による学習のしやすさが異なることが指摘されている。

Ho et al.(2020)のアルゴリズムを以下に示す。

3.3 推論

推論として、画像生成のアルゴリズムを提示する。

まず標準正規分布からノイズを1つ引き、$p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_{t}) = \mathcal{N}\left(\bold{x}_{t-1}; \mu_{\theta}(\bold{x}_{t}, t), \bold{\Sigma}_{\theta}(\bold{x}_{t}, t)\right)$に基づいてreverse processの計算を行う。

この時変数変換をすることで、$ \mu_{\theta}(\bold{x}_{t}, t) + \sigma_t \bold{z}_{t}$, $ \bold{z}_{t}=\mathcal{N}\left(\bold{0}, \bold{I}\right)$としてサンプリング出来る。また学習パートで記載したように平均は推定したノイズを用いて表現する。

推論アルゴリズム(Ho et al.(2020)より引用)

4. Diffusion Model 実装

では具体的な実装について最後に見ていきたい。実装はHugging FaceのブログThe Annotated Diffusion Modelを参考にするとよい。

いくつか重要なところのみピックアップしていく。

  • 具体的にはdenoiseするニューラルネットワークの実装、実際の学習・生成のコードは割愛し、理論との対応関係を明確にする。

まずはノイズスケジュールについての実装を見ていく。


def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start, beta_end, timesteps)

timesteps = 200
# define beta schedule
betas = linear_beta_schedule(timesteps=timesteps)

# define alphas
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)

# calculations for diffusion q(x_t | x_{t-1}) and others
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)

ここでは$T=200$を想定し、$\beta$を線形に増加させていくように設定する。また論文と同様に$\alpha = 1- \beta$として定義している。 さらにalphas_cumprodにおいて$\bar{\alpha}_t$を計算し、forward processのためのパラメータも用意している。

実際にforward processを定義すると下記のようになる。

def q_sample(x_start, t, noise=None):
    if noise is None:
        noise = torch.randn_like(x_start)

    sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x_start.shape
    )

    return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise

ややわかりにくいがextract関数を使って、適切な時刻のノイズパラメータの累積値を取り出すことで、 $ q\left(\bold{x}_{t} \mid \bold{x}_{0}\right) = \mathcal{N}\left( \sqrt{\bar{\alpha}_{t}}\bold{x}_{0}, \bar{\beta}_{t}\bold{I}\right) $を計算していることがわかる。

次にloss関数を定義する。

学習アルゴリズム(Ho et al.(2020)より引用)

def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
    if noise is None:
        noise = torch.randn_like(x_start)

    x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
    predicted_noise = denoise_model(x_noisy, t)

    if loss_type == 'l1':
        loss = F.l1_loss(noise, predicted_noise)
    elif loss_type == 'l2':
        loss = F.mse_loss(noise, predicted_noise)
    elif loss_type == "huber":
        loss = F.smooth_l1_loss(noise, predicted_noise)
    else:
        raise NotImplementedError()

    return loss

学習アルゴリズムにあるように、ニューラルネットワークにノイズを含んだデータと時点情報を入力し、ノイズを予測する。そして真のノイズとの誤差をlossとして定義する。

  • denoise_model(x_noisy, t)が$\epsilon_\theta$に対応している。
    • denoise_modelはU-Netを利用しているが、ここでは割愛する。
  • ここでは論文とやや異なり、正則化を加えたloss関数についても対応していることがわかる。

最後にデータ生成に関わるプログラムを確認する。


# calculations for posterior q(x_{t-1} | x_t, x_0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)


@torch.no_grad()
def p_sample(model, x, t, t_index):
    betas_t = extract(betas, t, x.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x.shape
    )
    sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)

    # Equation 11 in the paper
    # Use our model (noise predictor) to predict the mean
    model_mean = sqrt_recip_alphas_t * (
        x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
    )

    if t_index == 0:
        return model_mean
    else:
        posterior_variance_t = extract(posterior_variance, t, x.shape)
        noise = torch.randn_like(x)
        # Algorithm 2 line 4:
        return model_mean + torch.sqrt(posterior_variance_t) * noise

# Algorithm 2 but save all images:
@torch.no_grad()
def p_sample_loop(model, shape):
    device = next(model.parameters()).device

    b = shape[0]
    # start from pure noise (for each example in the batch)
    img = torch.randn(shape, device=device)
    imgs = []

    for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
        img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)
        imgs.append(img.cpu().numpy())
    return imgs

@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
    return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))

まずp_sample関数が$\bold{x}_{t}$から$\bold{x}_{t-1}$を求める関数になっている。

  • $p_{\theta}(\bold{x}_{t-1} \mid \bold{x}_t) = \mathcal{N}\left(\bold{x}_{t-1}; \mu_{\theta}(\bold{x}_{t}, t), \bold{\Sigma}_{\theta}(\bold{x}_{t}, t)\right)$

  • model_meanはこの数式に対応している。$\mu_\theta(\bold{x}_{t}, t) = \frac{1}{\sqrt{\alpha}_{t}}\left(\bold{x}_{t} - \frac{\beta_{t}}{\sqrt{\bar{\beta}_{t}}}\epsilon_{\theta}(\bold{x}_{t} , t)\right)$

    • この部分の導出は今後モデルパートの拡充の際に記載する。

  • 最後のifブロックはサンプリングのときに説明した変数変換するノイズ部分に対応する。

    • $ \mu_{\theta}(\bold{x}_t, t) + \sigma_t \bold{z}_t$, $ \bold{z}_t=\mathcal{N}\left(\bold{0}, \bold{I}\right)$

なお p_sample_loopはreverse processをすべての時刻で実施するための関数で、 sample関数は単純なラッパー関数である。

6. 参考文献